
At first blush, this sounds like we have to compare two infinite numbers, and how could you do that? Actually,
you can, but that is another story. The number of stars in the (observable) universe is large,
but can be estimated.
I did this before, and the number I got was about
7"100%" height=5 00000000000000000 or 1021 rounded up, give or take an order of magnitude.
So how about the sand? I don't live near a beach, so I got a handful of sand from the backyard. Now this
does not look like beach sand at all - there are big chunks, and grains down to the size of dust. Beach
sand is more uniform in size. So I poured the sand through a small tea sieve, and discarded the dust that
fell through. Then I poured the sand through the big flour sieve, and discarded what remained in the sieve.
What fell through were grains of fairly uniform size. This looked much better, and what's more, this was
countable.
I measured out 1/8th teaspoon onto a sheet of paper. Still too many grains to count. Using the same technique
as I used before with the children to count pumpkin seeds, I divided
the sand in half, then quarters, and finally into 1/8ths. This was a countable 350 grains, give or take a few.
(more text)
How many stars are there?
2000-2001 web projects
2003 web projects
HTML cribsheets: page 1,
and page 2
18 April 2003
|

Here in New Mexico, we get some spectacular rainbows. The reason is that when
it rains here, it is usually from isolated thunder storms, not from a
completely overcast sky. So chances are that the sun is also shining.
|
1)
The first step is to explain that waves can get bent as they are slowed down.
I use waves on the beach to clarify this: the question is, why is it that waves always
seem to roll straight towards the beach? After all, a little ways offshore the
orientation of
the waves is likely to be some random direction, unlikely to be parallel to the beach!
Here is a game I use to make the kids figure it out: On the floor, I mark with masking
tape a line where waves slow down (red line in the diagram). This is where the water depth
gets shallow, slowing
waves down. I line up 2 kids side by side, and they are holding the ends of a broomstick (the blue line).
The broomstick represents the crest of a wave. When the children walk forward, this
is like a wave rolling across the ocean in the direction of my beach which is marked on
the floor. The rules are this: when you are in the open ocean, you can take big steps,
but as soon as you cross the line, you have to take very small steps. When they approach
the beach straight on, nothing much happens, except that they slow down as they cross the
line. However, when they approach the beach at an angle, the student who croses the line
first will start making small steps before the other one does, and the broomstick
gets swung around a bit and now is more parallel to the beach. If the purple dots denote footsteps,
notice that the kid on the left takes one big step and 7 small ones, but the one on the right takes
4 big ones and only 3 small ones.
If the water gets even
shallower, and the waves are slowed even more, they get bent again and by the time
they wash ashore, all waves are pretty much parallel to the beach, no matter how
they started out.
|
 2)
The next step is to show that this same bending happens with light. For this I had a
rectangular plastic container, filled with water to which I added a few drops of
milk. When you shine your laser pointer onto the surface at a shallow angle, the
beam gets refracted and dives into the water at a steeper angle.
2)
The next step is to show that this same bending happens with light. For this I had a
rectangular plastic container, filled with water to which I added a few drops of
milk. When you shine your laser pointer onto the surface at a shallow angle, the
beam gets refracted and dives into the water at a steeper angle.
|
| 3)
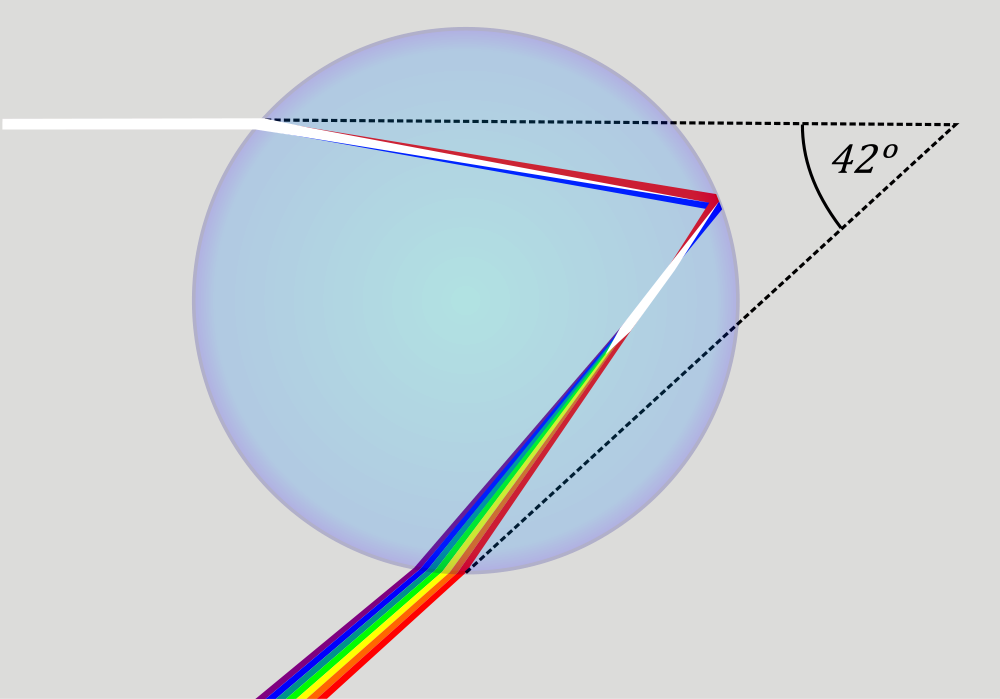
The next step is to draw on the board the standard picture of the rays in a water drop
that make the rainbow, see the second picture
on this page. The white light strikes the surface of the raindrop at an angle,
and some of it gets refracted, that is, it changes directon. The amount
of refraction is different for different colors (wavelengths) that make up the white
sunlight. Blue light gets bent a little more than rd light. Next, the light reflects
off the back of the raindrop, and when it comes to the surface ofthe drop one last time,
it gets refracted again, blue again a little more than red.
Most explanations of rainbows show a drawing such as the one on the right,
and then contain a sentence such as this one:
"The refracted light appears at an angle of 42° with respect to the incoming
sunlight" - more on that angle later.
|
|
4)
You can actually show this directly, with this simple setup: I hang
a 1 or 2-liter bottle filled with water from the top of the blackboard
(for example using a sharp hook
filed from a piece of coathanger and little cardboard standoff that holds the bottle
away from the board). Across the room I set up an (nowadays old-fashioned)
slide projector that shines
light onto the bottle. (I found that if you cover the lens of the projector with
some black paper with a vertical slit cut in it (1/4 - 1/2"), the rainbow colors
will be better defined). It also helps to have a dark background.

|

|
|
5)
Now if you look at the bottle at exactly the right angle,
namely 42 degrees to the left or the right, you can see the rainbow colors coming
from the bottle. You
can hold a piece of white paper there and see the rainbow colors, as well as the
fact that the inside of the rainbow is brighter than the outside. Just looking at the
bottle and moving around makes the cause of this brightness effect plain: at angles
to the inside
of the rainbow, you can see all kinds of reflections of the slide projector light,
and they are absent ar angles outside of the (primary) rainbow.
|


|
|
6)
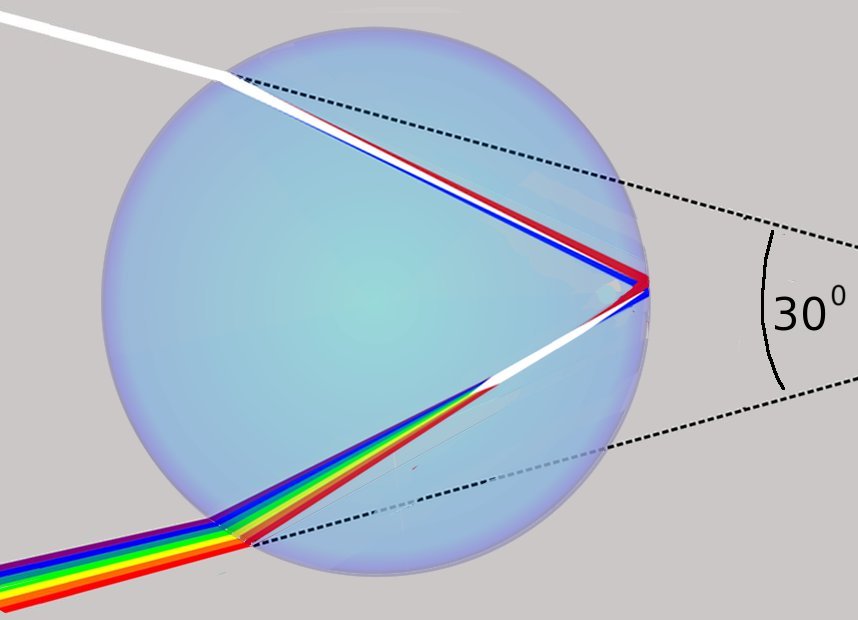
But what if I draw the diagram like this →,
with an opening angle of 30°, or 31°, or any
other angle? What's wrong with that?
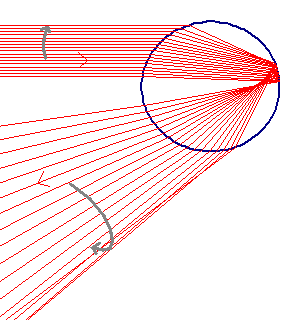 The answer is that these are all valid diagrams, and they all
occur at the same time. But all these rainbows at smaller angles overlap, and the overlap of ALL
colors result in the
reflection being white again... EXCEPT for the very last one at 42°.
(plot made using CERN's Root)
The answer is that these are all valid diagrams, and they all
occur at the same time. But all these rainbows at smaller angles overlap, and the overlap of ALL
colors result in the
reflection being white again... EXCEPT for the very last one at 42°.
(plot made using CERN's Root)
|
|
|
Things that don't work: (1) The bottle demo works fine, but it is a cylinder,
not a sphere. I tried to make a transparent sphere with a latex water balloon,
made more shiny with some vaseline. I could never observe the colors at the
rainbow angle.
|


|
|
| Things that don't work: (2) I made a contraption to produce a tabletop
rainshower. It is a platform with a vertical post. Along the post you can slide a
1-gallon can up and down. The bottom of the can has many small holes punched in
it. There is a pail to catch the water, and a little aquarium pump to pump it
back up. I set this
up in the sun (actually in a
sunbeam from my heliostat), and looked for
colorful sparkles in the falling droplets. No dice.
| 
|
Links:
30 October 2003 and regularly since then
|















